各位觀眾、各位大大們空幫哇～～～～～～
本來昨天說數學系列應該要結束了，
不過意外的找到一個叫 佩服數 的數，
哪泥搜勒～？
那我們再次有請維基大師為我們說明個！

https://zh.wikipedia.org/wiki/%E4%BD%A9%E6%9C%8D%E6%95%B8
佩服數
在數論中，佩服數（英文：Admirable numbers），是指若一個正整數除了本身外之所有的因數，
存在一個因數 d1，將其他不是本身、不是 d1 的因數相加後，再減掉 d1，若等於本身，我們就稱它為「佩服數」。
換句話說佩服數是計算一數的因數和，但其中一個因數是以相反數和其他因數相加，得到的值是自己本身的數。有這種性質的數雖未如完全數一般的完美，但仍被形容為「令人敬佩的」。

原來佩服數不像完全數一樣完美，但還是令人敬佩，故稱「佩服數」XD
長知識了XD

正片開始

今日素材：佩服數

這邊簡單舉個例，例如 12 因數有 1,2,3,4,6,12
就以上定義就是將不包含 12 的因數相加（且不包含其中一個因數 d1），
還再將相加結果再減掉 d1 ，
1(+2)+3+4+6 = 14 - 2 = 12，
則 12 為佩服數。

本日挑戰 Start

1. 先試寫因數相加邏輯

let basciNum = 12;
let factorSum = 1;

for ( let i=2; i<basciNum; i++ ){
    if ( basciNum%i == 0 ){
        factorSum += i;
    }
}

console.log(`factorSum: ${factorSum}`);

2. 加入佩服數判斷邏輯
   但這邊要注意，因數不包含 d1 相加還要再減 d1，
   所以想簡單一點就是 d1 減 2 次的意思。
   (因為我不小心搞錯邏輯過orz 少減一次之類的)

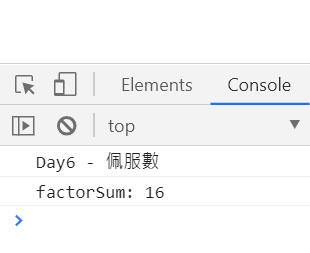
let basciNum = 30;
let factorSum = 0;

for ( let i=1; i<basciNum; i++ ){
    if ( basciNum%i == 0 ){
        factorSum += i;
    }
}

console.log(`factorSum: ${factorSum}`);

for ( let i=1; i<basciNum; i++ ){
    if ( basciNum%i === 0 ){
        if ( factorSum - i*2 === basciNum ){ // 因數相加再減掉因數*2 看是否等於本身
            console.log(`${basciNum} 是佩服數！`);
        }
    }
}

3. 再換一個數字 88 驗證看看

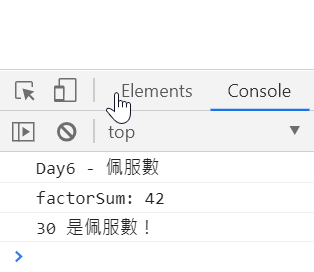
let basciNum = 88;
let factorSum = 0;

for ( let i=1; i<basciNum; i++ ){
    if ( basciNum%i == 0 ){
        factorSum += i;
    }
}

console.log(`factorSum: ${factorSum}`);

for ( let i=1; i<basciNum; i++ ){
    if ( basciNum%i === 0 ){
        if ( factorSum - i*2 === basciNum ){
            console.log(`${basciNum} 是佩服數！`);
        }
    }
}

4. 加入因數相對的邏輯，換成是佩服數的 40 試試看

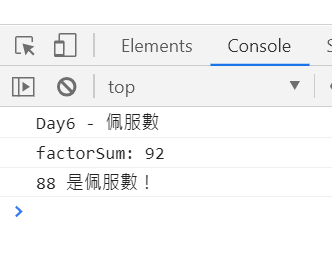
let basciNum = 40;
let factorSum = 0;

let endNum = basciNum;
for ( let i=1; i<endNum; i++ ){
    if ( basciNum%i === 0 ){
        factorSum += i;
        endNum = basciNum/i;
    }
}

console.log(`factorSum: ${factorSum}`);

endNum = basciNum;
for ( let i=1; i<endNum; i++ ){
    if ( basciNum%i === 0 ){
        if ( factorSum - i*2 === basciNum ){
            console.log(`${basciNum} 是佩服數！`);
        }
        endNum = basciNum/i;
    }
}

但發現 40 不會被判斷為佩服數，
只好多埋些 console.log 來看原因了QQ
(眼尖的大大可能已經知道怎麼回事了XD)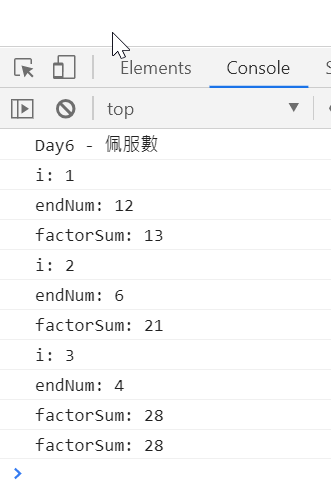

抓到了！
原因是第 1 個迴圈不可以從 1 開始，
不然在算因數加總時會連 12/1=12 都會加進去
第 2 個迴圈才要從 1 開始判斷。

5. 修正後，改成 30 試試看

let basciNum = 30;
let factorSum = 1;

let endNum = basciNum;
for ( let i=2; i<endNum; i++ ){ // 這邊改成從 2 開始
    if ( basciNum%i === 0 ){
        factorSum += i;
        factorSum += basciNum/i;
        endNum = basciNum/i;
    }
}

console.log(`factorSum: ${factorSum}`);

endNum = basciNum;
for ( let i=1; i<endNum; i++ ){
    if ( basciNum%i === 0 ){
        if ( factorSum - i*2 === basciNum ){
            console.log(`${basciNum} 是佩服數！`);
        }
        if ( factorSum - basciNum/i*2 === basciNum ){
            console.log(`${basciNum} 是佩服數！`);
        }
        endNum = basciNum/i;
    }
}

6. 外層再加上迴圈找更多佩服數看看，
   還有發現上面有 2 個 if 裡面做的事很像，
   因此將它合併在一個 if 裡面。

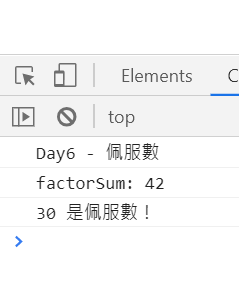
// let basicNum = 12;
let factorSum;
let admirableNumArray = []; 

for ( let basicNum=2; basicNum<=1000; basicNum++){
    factorSum = 1;
    let endNum = basicNum;
    for ( let i=2; i<endNum; i++ ){
        if ( basicNum%i === 0 ){
            factorSum += i;
            factorSum += basicNum/i;
            endNum = basicNum/i;
        }
    }

    endNum = basicNum;
    for ( let i=1; i<endNum; i++ ){
        if ( basicNum%i === 0 ){
            if ( factorSum - i*2 === basicNum || factorSum - basicNum/i*2 === basicNum ){
                console.log(`${basicNum} 是佩服數！`);
                admirableNumArray.push(basicNum);
                if ( basicNum%2 !== 0 ){
                    console.log(`${basicNum} 是奇數中的佩服數！`);
                }
            }
            endNum = basicNum/i;
        }
    }
}

console.log(`佩服數共有 ${admirableNumArray.length} 個`);

7. 邏輯寫對了以後，一樣來看個計算次數~

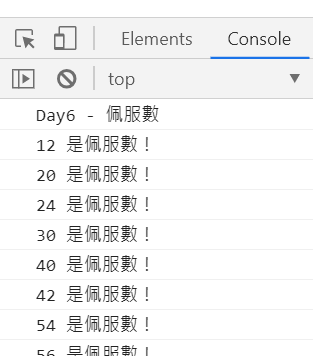
// let basicNum = 12;
let factorSum;
let admirableNumArray = []; 
let admirableOddNumArray = [];
let countTimes_1 = 0; // 前半段計算次數
let countTimes_2 = 0; // 後半段計算次數

for ( let basicNum=2; basicNum<1000; basicNum++){
    factorSum = 1;
    let endNum = basicNum;
    for ( let i=2; i<endNum; i++ ){
        countTimes_1++;
        if ( basicNum%i === 0 ){
            factorSum += i;
            factorSum += basicNum/i;
            endNum = basicNum/i;
        }
    }

    endNum = basicNum;
    for ( let i=1; i<endNum; i++ ){
        countTimes_2++;
        if ( basicNum%i === 0 ){
            if ( factorSum - i*2 === basicNum || factorSum - basicNum/i*2 === basicNum ){
                console.log(`${basicNum} 是佩服數！`);
                admirableNumArray.push(basicNum);
                if ( basicNum%2 !== 0 ){
                    console.log(`${basicNum} 是奇數中的佩服數！`);
                    admirableOddNumArray.push(basicNum);
                }
            }
            endNum = basicNum/i;
        }
        if ( admirableOddNumArray.length === 2 ){
            break;
        }
    }
}

console.log(`佩服數共有 ${admirableNumArray.length} 個`);
console.log(`奇佩服數共有 ${admirableOddNumArray.length} 個`);
console.log(`前半段計算次數 ${countTimes_1} 次`);
console.log(`後半段計算次數 ${countTimes_2} 次`);

8. 2 個迴圈跑的次數太多了！
   前半段計算次數 138190 次
   後半段計算次數 139188 次
   然後因數有位大大提醒我用根號就好，(其實我隱隱約約記得這件事orz)
   因此這邊改個比較一下。

// let basicNum = 12;
let factorSum;
let admirableNumArray = []; 
let admirableOddNumArray = [];
let countTimes_1 = 0; // 前半段計算次數
let countTimes_2 = 0; // 後半段計算次數

for ( let basicNum=2; basicNum<1000; basicNum++){
    factorSum = 1;
    let endNum = basicNum;
    for ( let i=2; i<=Math.sqrt(basicNum); i++ ){ // 因數改成找開根號以下內的數字就好
        countTimes_1++;
        if ( basicNum%i === 0 ){
            factorSum += i;
            factorSum += basicNum/i;
            endNum = basicNum/i;
        }
    }

    endNum = basicNum;
    for ( let i=1; i<=Math.sqrt(basicNum); i++ ){ // 因數改成找開根號以下內的數字就好
        countTimes_2++;
        if ( basicNum%i === 0 ){
            if ( factorSum - i*2 === basicNum || factorSum - basicNum/i*2 === basicNum ){
                console.log(`${basicNum} 是佩服數！`);
                admirableNumArray.push(basicNum);
                if ( basicNum%2 !== 0 ){
                    console.log(`${basicNum} 是奇數中的佩服數！`);
                    admirableOddNumArray.push(basicNum);
                }
            }
            endNum = basicNum/i;
        }
    }
}

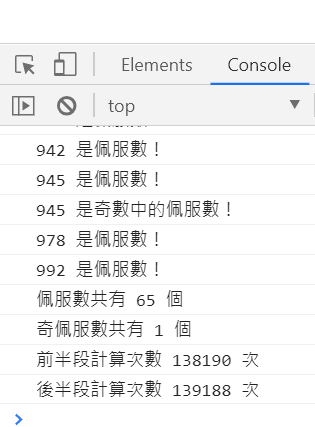
console.log(`佩服數共有 ${admirableNumArray.length} 個`);
console.log(`奇佩服數共有 ${admirableOddNumArray.length} 個`);
console.log(`前半段計算次數 ${countTimes_1} 次`);
console.log(`後半段計算次數 ${countTimes_2} 次`);

整個降超多！！！！！

[後記]

其實我有一個非常想改的地方，
程式我先用第一個迴圈算出因數總和，
再用第二個迴圈判斷因數總和減去因數x2，
光是因數就重複找了兩次.......
應該可以改成一個迴圈就能解決QAQ
但先將文章發出去再說orz
不過放心這絕對不是明天文章啦，
所以就～
大家明天見 && 大家加油 XD
終於又安然度過一天。